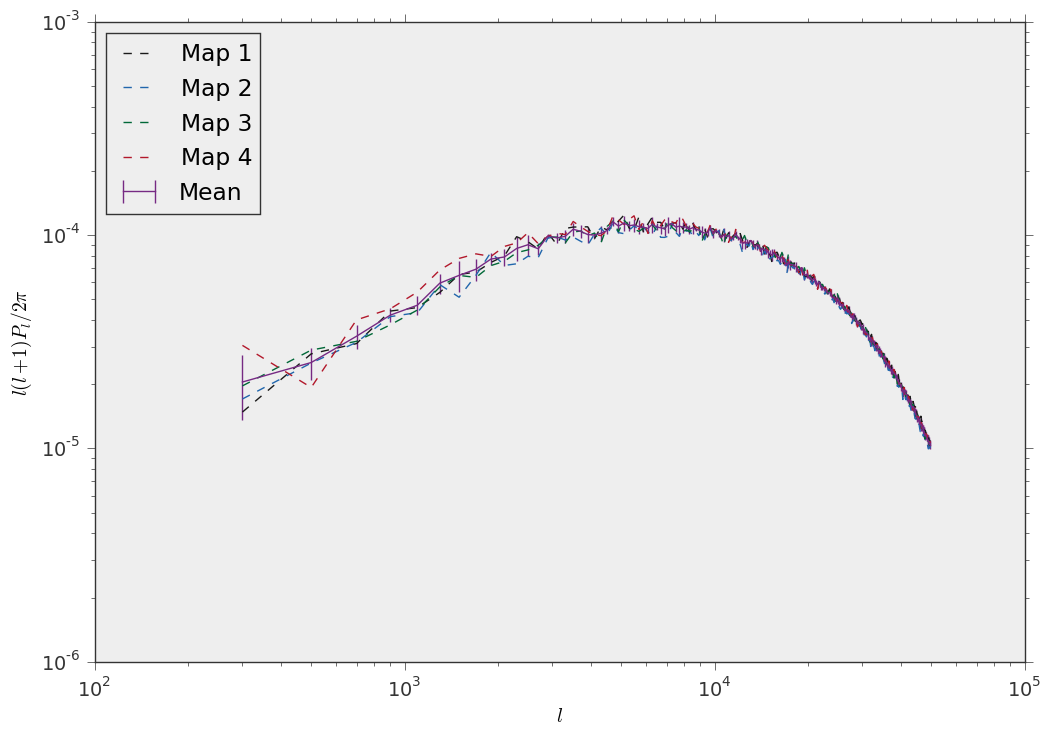
Measure the power spectrum of a convergence map (MPI)¶
When you need to measure the power spectrum of many different convergence maps (for example 1000 different realizations of a field of view), you are effectively measuring an Ensemble of quantities. lenstools provides Ensemble computing tools through the Ensemble class. This class supports parallel operations too through MPI, like in this example. First define a function that measures the power spectrum out of a single map:
#The operations on convergence maps are handled with the ConvergenceMap class
from lenstools import ConvergenceMap
def measure_power_spectrum(filename,l_edges):
conv_map = ConvergenceMap.load(filename)
l,Pl = conv_map.powerSpectrum(l_edges)
return Pl
This is the actual code:
from lenstools.statistics.ensemble import Ensemble
from lenstools.utils.decorators import Parallelize
import logging
import numpy as np
import matplotlib.pyplot as plt
logging.basicConfig(level=logging.DEBUG)
@Parallelize.masterworker
def main(pool):
l_edges = np.arange(200.0,50000.0,200.0)
l = 0.5*(l_edges[:-1] + l_edges[1:])
conv_ensemble = Ensemble.compute(["Data/conv1.fit","Data/conv2.fit","Data/conv3.fit","Data/conv4.fit"],callback_loader=measure_power_spectrum,pool=pool,l_edges=l_edges)
fig,ax = plt.subplots()
for n in range(len(conv_ensemble)):
ax.plot(l,l*(l+1)*conv_ensemble.iloc[n]/(2.0*np.pi),label="Map {0}".format(n+1),linestyle="--")
mean = conv_ensemble.mean(0)
errors = np.sqrt(conv_ensemble.covariance().values.diagonal())
ax.errorbar(l,l*(l+1)*mean/(2.0*np.pi),yerr=l*(l+1)*errors/(2.0*np.pi),label="Mean")
ax.set_xscale("log")
ax.set_yscale("log")
ax.set_xlabel(r"$l$")
ax.set_ylabel(r"$l(l+1)P_l/2\pi$")
ax.legend(loc="upper left")
plt.savefig("power_ensemble.png")
if __name__=="__main__":
main(None)
And this is the result