Constraining cosmological (and not) parameter spaces¶
This brief tutorial shows how to use lenstools to use the emulator and contour plotting features to produce publication quality confidence contour plots. This example has nothing to do with cosmology or weak lensing, but the methods are immediately transferrable to these fields. The tutorial is also available in this notebook.
First we need to set up the environment
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from lenstools.statistics.ensemble import Ensemble,Series
from lenstools.statistics.constraints import Emulator
from lenstools.statistics.contours import ContourPlot
The next step is to generate some fake training data (in a weak lensing analysis these will be provided by the simulations: the parameters will be the cosmological parameters, the features will be power spectra, etc…)
p = np.outer(np.arange(10.0),np.ones(2))
f = np.outer(np.arange(10.0)+0.1*2,np.ones(5))
emulator = Emulator.from_features(f,p,parameter_index=["alpha","beta"],feature_index=[r"$f_{0}$".format(n) for n in range(5)])
Next we generate some fake test feature to fit (in a weak lensing context these will be the actual data)
test_feature = Series(np.ones(5)*4.0 + 0.05*np.random.randn(5),index=emulator[["features"]].columns)
We need to assume a particular form for the feature covariance matrix: the simplest one is a diagonal form
features_covariance = Ensemble(np.eye(5)*0.5,index=test_feature.index,columns=test_feature.index)
Next we train the emulator (basically set it up to interpolate the features between the training points provided)
emulator.train()
We then build a grid of possible parameter combinations to assign to the test_feature, and we evaluate the score of each of these parameter combinations
#Grid of parameters
g = np.arange(0.0,10.0,0.5)
p = np.array(np.meshgrid(g,g,indexing="ij")).reshape(2,400).T
test_parameters = Ensemble(p,columns=emulator.parameter_names)
#Scores are chi squared: the probability is exp(-0.5*chi2)
scores = emulator.score(parameters=test_parameters,observed_feature=test_feature,features_covariance=features_covariance)
scores['features'] = np.exp(-0.5*scores['features'])
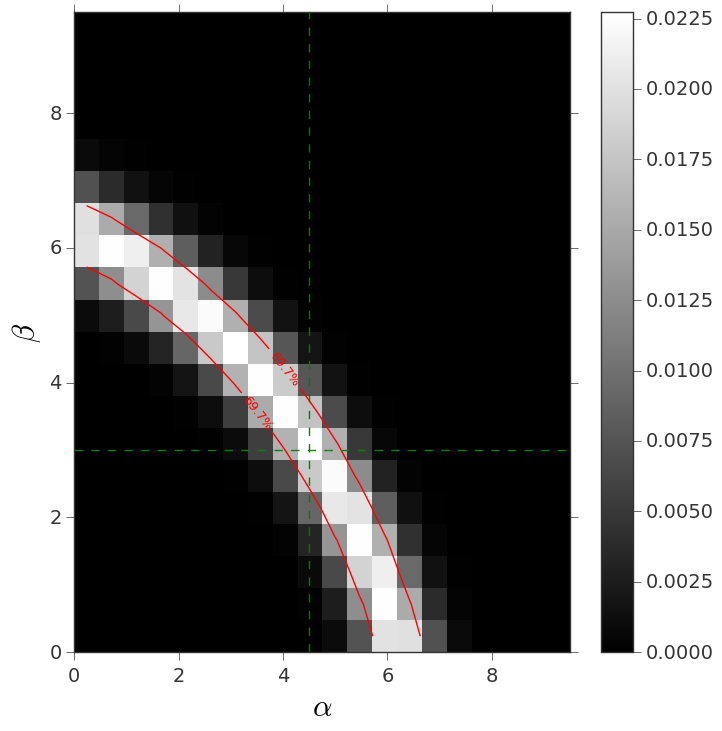
Finally we plot the (alpha,beta) confidence contours
contour = ContourPlot.from_scores(scores,parameters=emulator.parameter_names,plot_labels=[r"$\alpha$",r"$\beta$"])
contour.show()
contour.getLikelihoodValues([0.684],precision=0.1)
contour.plotContours(colors=["red"])
contour.labels()
contour.savefig("contour_example.png")
This is how the result looks like